There’s a lot of hubbub lately over AlphaFold (and other Machine Learning protein structure prediction methods) running out of data. We’ve exhausted the publicly available resources for protein structure data, so pharmaceutical companies are pooling up their vast collection of private data to get a leg up.

Some have argued that these pharmaceutical companies should open-source their troves of data for the public benefit, and I agree. This would be a good and non-zero-sum thing for them to do—they should have done it already.

But, unfortunately, I suspect that this data is not going to make that much of a difference. AlphaFold does have a data problem, but it’s not that we need more of what we already have. We need something altogether different.

I have no formal art education, but I’ve made art—most of it pretty bad, with some small flashes of beauty. How much good art I’ve made in my life depends on what “art” is. I’ve never had much of a felicity for visual art, but, some of the music I’ve made and composed certainly counts. What about meals I’ve cooked? Hack-y poems that nonetheless feel genuine—candid and personal—products of myself from a time and place? What about a conference seminar, or a lecture series on Physical Biochemistry?

Artificial Intelligence (AI) and Machine Leaning (ML) have very publicly shaken up the Art World and — for lack of a better catch-all term — the world of the Written Word: Hollywood unions fought a long, public battle to (amongst many other things) keep AI/ML out of writers rooms; artists and graphic designers on social media endlessly lament the theft of their work by companies who trained their AI/ML models on it without permission, and whose models generate near-copies of their work if prompted specifically enough; writers have found that AI/ML models can mimic their voice and style in clunky but uncanny and foreboding ways. Though the models remain relatively crude and largely unprofitable, for now, there is nevertheless a looming question of whether human dominance in these fields will survive the century, or even the decade.

A lesser known but perhaps more insidious infiltration of AI/ML is happening in the world of science. Researchers have been caught using Large Language Models (LLMs) to fill in parts of their scientific papers and AI/ML methods are being used to fake scientific figures in ways that are hard to spot using standard fraud-detection techniques. Despite getting more positive press, most insidious of all is the rise of AI/ML algorithms as earnest scientific modeling tools. Peruse the pages of scientific journals these days and you’ll be hard pressed to find an issue that doesn’t include a paper using an AI/ML algorithm as a sort of ersatz scientific model. The popular science press is flooded with articles trumpeting the supposed success of AI/ML in fields like medicine, education, and nuclear fusion. These models are now so common that researchers and the broader scientifically-engaged public no longer bat an eye.

I’d argue that we’re watching, across the board, is not just a technological hype cycle but a wholesale abandonment of principle: a deep philosophical battle that we’re all conscripted in. Artists, writers, scientists, the broader public—we’re all due for a wake up call. We’re in the early stages of this fight, but the machines and their allies are winning.

The following is instructions for the bare minimum in working with diffuse scattering data: viewing an .mtz file of diffuse scattering.

We’ll create a conda environment, then create a python .py file for viewing the .mtz file, and then run it

I’ve been trying to write more — mostly journaling, with a few little side projects here and there. It’s been a pleasant surprise to see just how much can come pouring out when I give myself the time and mental space. Memories that haven’t surfaced in years; opinions I didn’t know I had or (through writing) found I can’t actually justify; petty grievances and imagined slights that evaporate at the slightest introspection.

I’m more than a little ashamed to admit that at this point in my life, “giving myself time and mental space” basically equates to taking a break from being on my phone. 

“The Ewald Sphere”

If you need enticement to stick with this – this is probably the most beautiful piece of theory I’ve ever come across ✨it’s really something special.

Last time, we found that when an X-ray beam scatters through a volume of electron density, the intensity we measure in the far field is proportional to the squared magnitude of the form factor:

Let’s review a little…

“The Phase Problem”, or, “You didn’t think Mother Nature was gonna let us off that easy, did you?”

Last time we talked about how an incident X-ray beam is scattered by the electrons around atoms, and why the cumulative effect of the scattering is such that the electrons perform the Fourier Transform!

Let’s discuss what this means in practice.

We started with an X-ray wave traveling in a direction, defined by a wavevector, \(\mathbf{k}\).

Electrons scatter that wave, so it radiates out spherically, at all angles defined by \(\mathbf{k}'\) (a vector at an angle \(2\theta\) to the original wavevector, \(\mathbf{k}\))

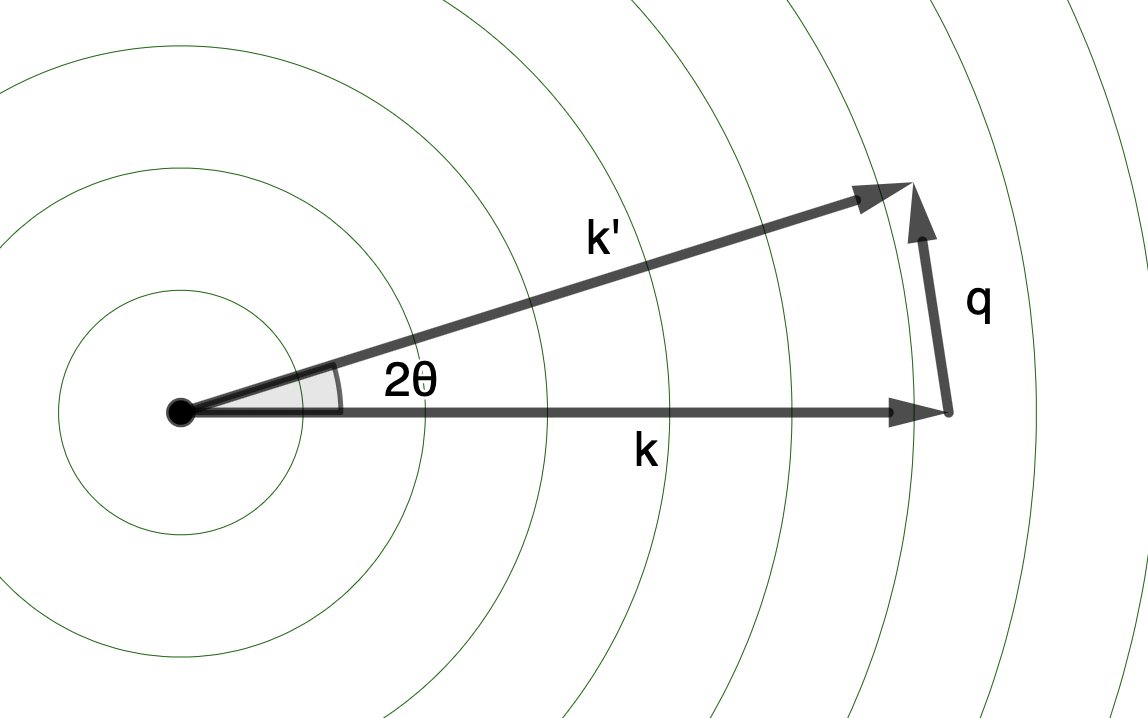
We choose to express the scattering through the “scattering vector” \(\mathbf{q}\), the vector that points from the tip of \(\mathbf{k}\) to the tip of \(\mathbf{k}'\).

Sweeping through all angles, the collection of these \(\mathbf{k}'\)s forms a sphere.

“How electrons perform the Fourier Transform”

Warning: this is going to require a good bit of physics and math.

If that’s not your thing, fair enough, feel free to bail.

But I’m going to try to make this as palatable as I can.

So give it a go, if you’re feeling up to it.

Let’s start with the math of how crystallography really works.

X-rays (wavelength λ=10⁻¹¹-10⁻⁸ m; energy 0.02-20 keV) scatter, elastically, off of electrons bound to atoms, producing spherical waves of the same wavelength.

We can describe the direction of traveling wave using a “wavevector” \(\mathbf{k}\), with the magnitude of the vector equal to the “wavenumber”, \(\frac{2\pi}{\lambda}\), and the direction pointing in the direction of propagation. For the incident X-ray plane wave, there is a single, definite wavevector (\(\mathbf{k}\)). For the scattered wave, there are many, equivalent wavevectors (\(\mathbf{k}'\)), one for each scattering angle.

The difference in direction between the incident (\(\mathbf{k}\)) and scattered (\(\mathbf{k'}\)) wavevectors is given by the “scattering vector”, \(\mathbf{q} = \mathbf{k'} - \mathbf{k}\).

Its magnitude is given by \(\lvert \mathbf{q} \rvert = \frac{4 \pi \sin( \theta )}{ \lambda }\), where \(2 \theta\) is the scattering angle.

If there are multiple electrons scattering the incident wave, separated by a vector \(\mathbf{r}\), the scattered waves will differ by a phase shift given by the dot product of \(\mathbf{q}\) and \(\mathbf{r}\): \(\Delta \phi = \mathbf{q} \cdot \mathbf{r}\).

Hey, welcome to my site. work in progress